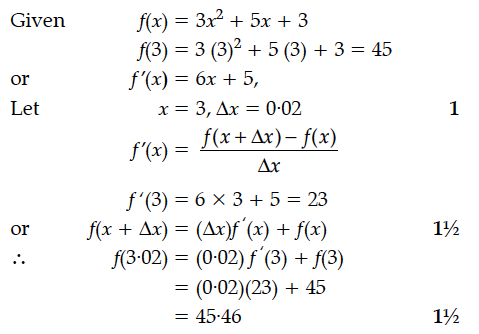
Find the point on the curve y = x³ – 11x + 5 at which the equation of tangent is y = x – 11.
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
Find the points on the curve x² + y² – 2x – 3 = 0 at which tangent is parallel to x-axis.
Show that the equation of tangent to the parabola y² = 4ax at (x₁, y₁) is yy₁ = 2a(x + x₁).
Let f, g : R → R be two functions defined as f (x) = |x| + x and g (x) = |x| – x for all x ∈ R.Then find fog and gof.
A speaks truth in 60% of the cases, while B in 90% of cases. In what percent of cases are they likely to contradict each other in stating the same fact ? In the cases of contradiction do you think, the statement of B will carry more weight as he speaks truth in more number of cases than A ?
The amount of pollution content added in air in a city due to x-diesel vehicles is given by p(x) = 0·005x³ + 0·02x² + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added.