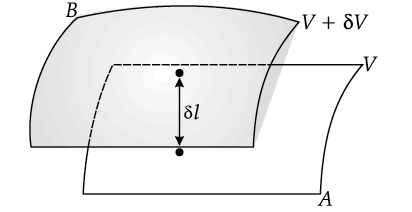
Two closely spaced equipotential surfaces A and B with potentials V and V + , (where is the change in V), are kept distance apart as shown in the figure. Deduce the relation between the electric field and the potential gradient between them. Write the two important conclusions concerning the relation between the electric field and electric potentials.

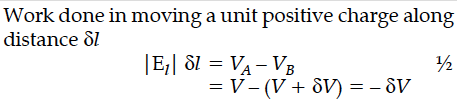

Three concentric metallic shells A, B and C of radii a, b and c (a < b < c) have surface charge densities +σ, –σ and +σ respectively as shown in the figure.
A test charge q is moved without acceleration from A to C along the path from A to B and then from B to C in electric field E as shown in the figure.
Define an equipotential surface. Draw equipotential surfaces :
(i) in the case of a single point charge and
(ii) in a constant electric field in z-direction. Why the equipotential surfaces about a single charge are not equidistant ?
(iii) Can electric field exist tangential to an equipotential surface ? Give reason.
Write two properties of equipotential surfaces. Depict equipotential surfaces due to an isolated point charge. Why do the equipotential surfaces get closer as the distance between the equipotential surfaces and the source charge decreases ?
(i) Write two properties by which electric potential is related to the electric field.
(ii) Two point charges q₁ and q₂ separated by a distance of r₁₂ are kept in an external electric field. Derive an expression for the potential energy of the system of two charges in the field.
(i) Three point charges q, – 4q and 2q are placed at the vertices of an equilateral triangle ABC of side ‘l’ as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
In a region of constant potential,
(a) the electric field is uniform
(b) the electric field is zero
(c) there can be no charge inside the region
(d) the electric field shall necessarily change, if a charge is placed outside the region
A battery of emf 10 V and internal resistance 3 ohm is connected to a resistor. If the current in the circuit is 0.5 A, find :
(i) the resistance of the resistor;
(ii) the terminal voltage of the battery.
N spherical droplets, each of radius r, have been charged to have a potential V each. If all these droplets were to coalesce to form a single large drop, what would be the potential of this large drop ?
(It is given that the capacitance of a sphere of radius x equals
A 9 V battery is connected in series with a resistor. The terminal voltage is found to be 8 V. Current through the circuit is measured as 5 A. What is the internal resistance of the battery?
A network of resistors is connected to a 16 V battery with internal resistance of 1 Ω, as shown in the following figure. Compute the equivalent resistance of the network.
The figure shows a plot of terminal voltage ‘V’ versus the current ‘i’ of a given cell. Calculate from the graph
(i) emf of the cell and (ii) internal resistance of the cell.
A capacitor ‘C’, a variable resistor ‘R’ and a bulb ‘B’ are connected in series to the ac mains in circuit as shown. The bulb glows with some brightness.How will the glow of the bulb change if
(i) a dielectric slab is introduced between the plates of the capacitor, keeping resistance R to be the same;
(ii) the resistance R is increased keeping the same capacitance ?
In a series LCR circuit, obtain the conditions under which
(i) the impedance of the circuit is minimum, and
(ii) wattless current flows in the circuit.
