(a) Define the term ‘conductivity’ of a metallic wire. Write its SI unit.
(b) Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in terms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E.
(b) Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in terms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E.
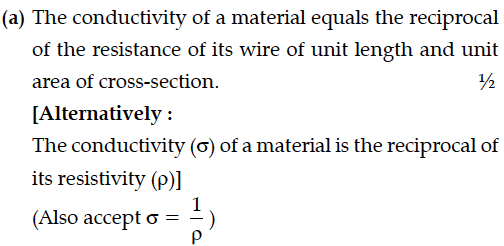

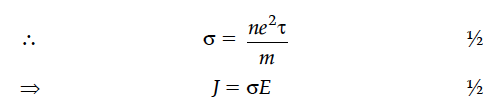
Define the term current density of a metallic conductor. Deduce the relation connecting current density (J) and the conductivity σ of the conductor, when an electric field E, is applied to it.
What is relaxation time ? Derive an expression for resistivity of a wire in terms of number density of free electrons and relaxation time.
Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons ? Use this relation to deduce the expression for the electrical resistivity of the material.
Using the concept of drift velocity of charge carriers in a conductor, deduce the relationship between current density and resistivity of the conductor.
Draw a plot showing the variation of resistivity of a (i) conductor and (ii) semiconductor, with the increase in temperature. How does one explain this behaviour in terms of number density of charge carriers and the relaxation time ?
A 10 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 38Ω as shown in the figure. Find the value of the current in the circuit.
(i) Derive an expression for drift velocity of free electrons.
(ii) How does drift velocity of electrons in a metallic conductor vary with increase in temperature ? Explain.
Derive an expression for electric field of a dipole at a point on the equatorial plane of the dipole. How does the field vary at large distances?
First a set of n equal resistors of R each is connected in series to a battery of emf E and internal resistance R. A current I is observed to flow. Then the n resistors are connected in parallel to the same battery. It is observed that the current becomes 10 times. What is n ?
A particle, having a charge +5 µC, is initially at rest at the point x = 30 cm on the x-axis. The particle begins to move due to the presence of a charge Q that is kept fixed at the origin. Find the kinetic energy of the particle at the instant it has moved 15 cm from its initial position if
(a) Q = +15 µC and
(b) Q = – 15 µC
(i) An electric dipole is kept first to the left and then to the right of a negatively charged infinite plane sheet having a uniform surface charge density. The arrows p₁ and p₂ show the directions of its electric dipole moments in the two cases.
A sinusoidal voltage of peak value 10 V is applied to a series LCR circuit in which resistance,capacitance and inductance have values of 10 Ω,1 µF and 1 H respectively. Find
(i) the peak voltage across the inductor at resonance
(ii) quality factor of the circuit.
The temperature coefficient of resistivity, for two materials A and B, are 0.0031 / °C and 0.0068 / °C respectively.
Two resistors R1 and R2, made from materials A and B, respectively, have resistances of 200 Ω and 100 Ω at 0°C. Show on a diagram, the 'colour code', of a carbon resistor, that would have a resistance
equal to the series combination of R1 and R2, at a temperature of 100°C.
(Neglect the ring corresponding to the tolerance of the carbon resistor).
(i) When an ac source is connected to an ideal capacitor show that the average power supplied by the source over a complete cycle is zero.
(ii) A lamp is connected in series with a capacitor.Predict your observation when the system is connected first across a dc and then an ac source.What happens in each case if the capacitance of the capacitor is reduced ?
