State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive.
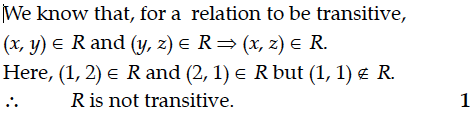
State the reason why the Relation R = {(a, b) : a ≤ b²} on the set R of real numbers is not reflexive.
How many equivalence relations on the set {1, 2, 3} containing (1, 2) and (2, 1) are there in all ?Justify your answer.
Check whether the relation R in the set R of real numbers, defined by R = {(a, b) : 1 + ab > 0}, is reflexive, symmetric or transitive.
Show that a function f : R → R given by f(x) =ax + b,a, b ∈ R, a ≠ 0 is a bijective.
Let R be the equivalence relation in the set A = {0, 1, 2, 3, 4, 5} given by R = {(a, b) : 2 divides (a –b)}. Write the equivalence class [0].
Let R={(a,a³): a is a prime number less than 5} be a relation. Find the range of R.
Find the differential equation representing the family of curves where A and B are arbitrary constants.
