For a 2 x 2 matrix, A = [aij] whose elements are given by aij = i/j, write the value of a12.
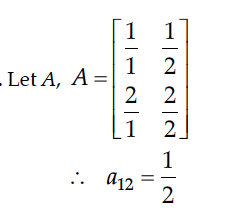
For a 2 × 2 matrix A = [ aij ], whose elements are given by aij=(i+2j)24 , write the value of a21.
If A is a 3 × 3 matrix, whose elements are given by aij=13|−3i+j| , then write the value of a23.
The elements aij of a 3 × 3 matrix are given by aij=12|−3i+j|.. Write the value of element a32.
Write the element a23 of a 3 × 3 matrix A = (aij) whose elements aij are given by
aij=|i−j|2
Let A and B are matrices of order 3 x 2 and 2 x 4 respectively. Write the order of matrix (AB).
If f : R → R is defined by f(x) = 3x + 2, then define f [f(x)].
State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive.
Let A = {1, 2, 3, 4}. Let R be the equivalence relation on A × A defined by (a, b)R(c, d) if a + d = b + c. Find the equivalence class [(1,3)].
If →a and →b are two unit vectors such that →a +→b is also a unit vector, then find the angle between →a and →b
