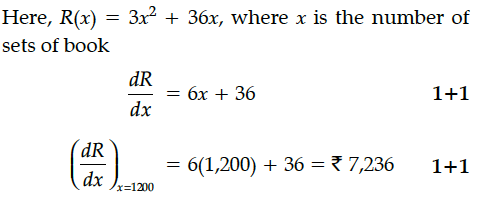
The total cost associated with provision of free mid-day meals to x students of a school in primary classes is given by C(x) = 0·005x³ – 0·02x² + 30x + 50. If the marginal cost is given by rate of change of total cost, write the marginal cost of food for 300 students.
The total revenue received from the sale of x units of a product is given by R(x) = 3x² + 36x + 5 in rupees. Find the marginal revenue when x = 5, where by marginal revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant.
The amount of pollution content added in air in a city due to x-diesel vehicles is given by p(x) = 0·005x³ + 0·02x² + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added.
The length x, of a rectangle is decreasing at the rate of 5 cm/minute and the width y, is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rate of change of the area of the rectangle.
If C = 0·003x³ + 0·02x² + 6x + 250 gives the amount of carbon pollution in air in an area on the entry of x number of vehicles, then find the marginal carbon pollution in the air, when 3 vehicles have entered in the area.
The radius r of a right circular cone is decreasing at the rate of 3 cm/minute and the height h is increasing at the rate of 2 cm/minute. When r = 9 cm and h = 6 cm, find the rate of change of its volume.
The radius r of a right circular cylinder is increasing at the rate of 5 cm/min and its height h, is decreasing at the rate of 4 cm/min. When r= 8 cm and h = 6 cm, find the rate of change of the volume of cylinder.
Solve the following differential equation. (1 + y²) (1 + log |x|) dx + x dy = 0
A problem in mathematics is given to 4 students A, B, C, D. Their chances of solving the problem, respectively, are 1/3, 1/4, 1/5 and 2/3. What is the probability that
(i) the problem will be solved ?
(ii) at most one of them solve the problem ?
Consider f : given by f(x) = x² + 4 Show that f is invertible with the inverse of f given by = , where is the set of all nonnegative real numbers.
Find the equations of the normal to the curve x² = 4y which passes through the point (1, 2).
Find the particular solution of the following differential equation :
Three schools A, B and C organised a fete (mela) collecting funds for flood victims in which they sold hand-helds fans, mats and toys made from recycled material, the sale price of each being ₹ 25, ₹ 100 and ₹ 50 respectively. The following table shows the number of articles of each type sold :