Three schools A, B and C organised a fete (mela) collecting funds for flood victims in which they sold hand-helds fans, mats and toys made from recycled material, the sale price of each being ₹ 25, ₹ 100 and ₹ 50 respectively. The following table shows the number of articles of each type sold :
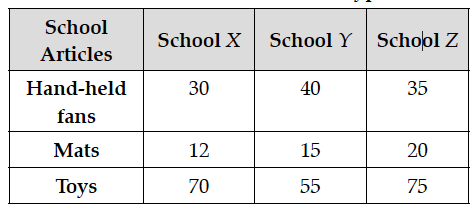
Using matrices, find the funds collected by each school by selling the above articles and the total funds collected. Also write any one value generated by the above situation.

Using matrices, find the funds collected by each school by selling the above articles and the total funds collected. Also write any one value generated by the above situation.

In a parliament election, a political party hired a public relations firm to promote its candidates in three ways — telephone, house calls and letters. The cost per contact (in paise) is given in matrix A as
To promote the making of toilets for women, as organisation tried to generate awareness through (i) house calls (ii) letters and (iii) announcements.
The cost for each mode per attempt is given below :
(i) ₹ 50 (ii) ₹ 20 (iii) ₹ 40
The number of attempts made in three villages X, Y and Z and given below :
A trust fund has ₹ 35,000 is to be invested in two different types of bonds. The first bond pays 8% interest per annum which will be given to orphanage and second bond pays 10% interest per annum which will be given to an N.G.O. (Cancer Aid Society). Use matrix multiplication, determine how to divide ₹ 35,000 among two types of bonds if the trust fund obtains an annual total interest of ₹ 3,200.
To raise money for an orphanage, students of three schools A, B and C organized an exhibition in their locality, where they sold paper bags, scrap-books and pastel-sheets made by them using recycled paper at the rate of ₹ 20, ₹ 15 and ₹ 10 per unit respectively. School A sold 25 paper bags, 10 scrap-books and 30 pastel-sheets. School B sold 20 paper-bags, 15 scrap-books and 30 pastel-sheets. While school C sold 25 paper-bags, 18 scrap-books and 35 pastel-sheets. Using matrices, find the total amount raised by each school.
Find the equation of tangents to the curve y = x³ + 2x – 4 which are perpendicular to the line x + 14y – 3 = 0.
Solve the following differential equation :
(1 + x²) dy + 2xy dx = cot x dx, (x ≠ 0)
Find the equation of the tangent to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at point x = 1, y = 0.
Let f : N → N be defined as
for all n ∈ N. State whether the function f is
bijective. Justify your answer.
Find the particular solution of the differential equation given that y = 0 when
