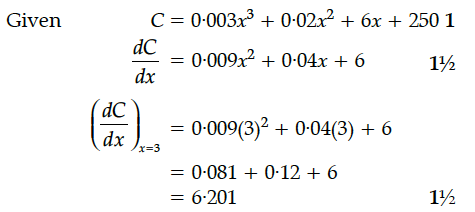
For the curve y = 5x – 2x³, if x increases at the rate of 2 units/sec, then find the rate of change of the slope of the curve when x = 3.
The amount of pollution content added in air in a city due to x-diesel vehicles is given by p(x) = 0·005x³ + 0·02x² + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added.
If the radius of sphere is measured as 9 cm with an error of 0.03 cm, then find the approximate error in calculating its surface area.
The volume of a cube is increasing at the rate of 9 cm³/sec. How fast is the surface area increasing when the length of an edge is 10 cm.
The side of an equilateral triangle is increasing at the rate of 2 cm/s. At what rate is its area increasing when the side of the triangle is 20 cm ?
The volume of a sphere is increasing at the rate of 8 cm³/sec. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
Find the equation of the normal at a point on the curve x² = 4y which passes through the point (1, 2). Also find the equation of the corresponding tangent.
Find the equations of the tangent and normal to the curve at the point .
A trust fund has ₹ 35,000 is to be invested in two different types of bonds. The first bond pays 8% interest per annum which will be given to orphanage and second bond pays 10% interest per annum which will be given to an N.G.O. (Cancer Aid Society). Use matrix multiplication, determine how to divide ₹ 35,000 among two types of bonds if the trust fund obtains an annual total interest of ₹ 3,200.
Find the particular solution of the differential equation satisfying the given condition given that y = 1, when x = 0.
Find the particular solution of the following differential equation :
given that y = 1, when x = 0.