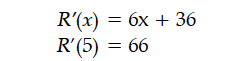
The length x, of a rectangle is decreasing at the rate of 5 cm/minute and the width y, is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rate of change of the area of the rectangle.
For the curve y = 5x – 2x³, if x increases at the rate of 2 units/sec, then find the rate of change of the slope of the curve when x = 3.
The radius r of a right circular cone is decreasing at the rate of 3 cm/minute and the height h is increasing at the rate of 2 cm/minute. When r = 9 cm and h = 6 cm, find the rate of change of its volume.
The volume of a sphere is increasing at the rate of 8 cm³/sec. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
The radius r of a right circular cylinder is increasing at the rate of 5 cm/min and its height h, is decreasing at the rate of 4 cm/min. When r= 8 cm and h = 6 cm, find the rate of change of the volume of cylinder.
A particle moves along the curve 6y = x³ + 2. Find the points on the curve at which y-coordinate is changing 2 times as fast as x-coordinate.
Find the equation of the normal at a point on the curve x² = 4y which passes through the point (1, 2). Also find the equation of the corresponding tangent.
If P(A) = 0.4, P(B) = p, P(A U B) = 0.6 and A and B are given to the independent events, find the value of ‘p’.
The radius r of a right circular cylinder is decreasing at the rate of 3 cm/min. and its height h is increasing at the rate of 2 cm/min. When r =7 cm and h = 2 cm, find the rate of change of the volume of cylinder.
A balloon, which always remains spherical, has a variable diameter . Find the rate of change of its volume with respect to x.
If x changes from 4 to 4·01, then find the approximate change in log x.
If A and B are two independent events, prove that A’ and B are also independent.
A die, whose faces are marked 1, 2, 3 in red and 4, 5, 6 in green, is tossed. Let A be the event “number obtained is even” and B be the event “number obtained is red”. Find if A and B are independent events.