Question

Using properties of determinants, prove that following : $\begin{vmatrix}a+x & y & z \\ x & a+y & z \\ x & y & a+z\end{vmatrix}$ = $a^{2}(a+x+y+z).$

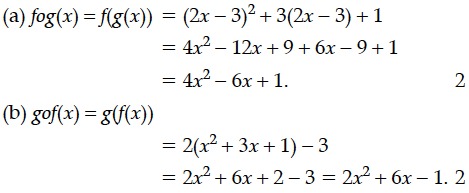
If the function f : R → R be defined by f(x) = 2x – 3 and g : R → R by g(x) = x³ + 5, then find fog and show that fog is invertible. Also, find (fog)⁻¹, hence find (fog)⁻¹(9).

Find a vector of magnitude 5 units and parallel to the resultant of $\stackrel{\rightarrow}{a}\$ = $2\stackrel{\wedge}{i}+3\stackrel{\wedge}{j} -\stackrel{\wedge}{k}$ and $\stackrel{\rightarrow}{b}\$ = $\stackrel{\wedge}{i}-2\stackrel{\wedge}{j} +\stackrel{\wedge}{k}$.

Find the equation of tangents to the curve y = x³ + 2x – 4 which are perpendicular to the line x + 14y – 3 = 0.

Find : $\textstyle\int$${\frac{x^{2}}{x^{4}+x^{2}-2}}d x$

If A = $\left(\begin{array}{l l }1 & -1 \\ 2 & -1\end{array}\right)$ , B = $\left(\begin{array}{l l }a & 1 \\ b & -1\end{array}\right)$ and (A + B)² = A²+ B², then find the values of a and b.

Using properties of determinants, prove that : $\begin{vmatrix}a+b+2c & a & b \\ c & b+c+2a & b \\ c & a & c+a+2b\end{vmatrix}$ = $2(a+b+c)^{3}.$