If E and F are two events such that P(E) = 1/4, P(F) = 1/2 and P(E ∩ F) = 1/8, find
(i) P(E or F)
(ii) P(not E and not F).
(i) P(E or F)
(ii) P(not E and not F).
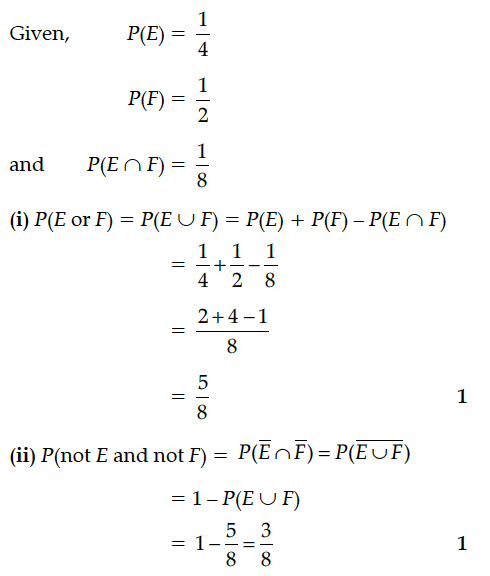
If E and F be two events such that P(E) = 1/3, P(F) = 1/4, find P(E U F) if E and F are independent events.
If A and B are two events such that P(A) = 0.4, P(B) = 0.8 and P(B/A) = 0.6, then find P(A/B).
If A and B are two independent events such that P(A' ∩ B)= 2/15 and P(A ∩ B')= 1/6, then find P(A) and P(B).
If A and B are any two events such that P(A) + P(B) – P(A and B) = P(A), then
(a) P(B|A) = 1
(b) P(A|B) = 1
(c) P(B|A) = 0
(d) P(B|A) = 0
Form the differential equation of all circles which is tough the x-axis at the origin.
If A and B are two independent events, prove that A’ and B are also independent.
The position vectors of points A, B and C are , and respectively. If C divides the line segment joining A and B in the ratio 3 : 1, find the values of λ and μ.
A die, whose faces are marked 1, 2, 3 in red and 4, 5, 6 in green, is tossed. Let A be the event “number obtained is even” and B be the event “number obtained is red”. Find if A and B are independent events.
