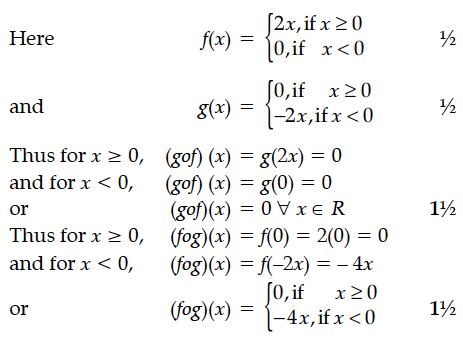
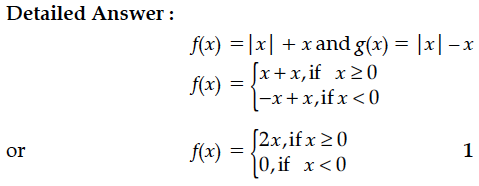
If f : R → R and g : R → R are given by f(x) = sin x and g(x) = 5x² then find gof(x)
Let f : R → R be defined by f(x) = 3x² – 5 and g : R → R be defined by g(x) = find gof(x) .
Let A = {1, 2, 3, . ...., 9} and R be the relation in A × A defined by (a, b) R (c, d) if a + d =b + c for (a, b), (c, d) in A × A. Prove that R is an equivalence relation. Also obtain the equivalence class [(2, 5)].
Show that f : N → N, given by f(x) = |``x+1, if x is odd x- 1, if x is even is both one-one and onto.``|
A bag contains (2n + 1) coins. It is known that (n – 1) of these coins have a head on both sides, whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed. If the probability that the toss results in a head is 31/42, determine the value of n.
Show that the relation S in the set R of real numbers defined as S = {(a, b) : a, b ∈ R and a ≤ b³} is neither reflexive nor symmetric nor transitive.
Show that the function f in A = defined as f(x) = is one-one and onto. Hence find