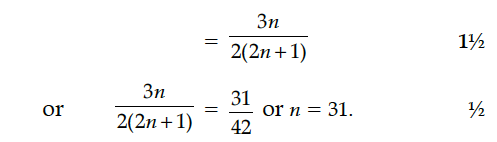
A box contains 50 bolts and 50 nuts. Half of the bolts and nuts are rusted. If two items are drawn with replacement, what is the probability that either both are rusted or both are bolts.
One bag contains 3 red and 5 black balls. Another bag contains 6 red and 4 black balls. A ball is transferred from first bag to the second bag and then a ball is drawn from the second bag. Find the probability that the ball drawn is red.
A and B throw a pair of dice alternately. A wins the game if he gets a total of 9 and B wins if he gets a total of 7. If A starts the game, find the probability of winning the game by B.
A and B throw a pair of dice alternately. A wins the game if he gets a total of 7 and B wins the game if he gets a total of 10. If A starts the game, then find the probability that B wins.
A speaks truth in 75% of the cases, while B in 90% of the cases. In what percent of cases are they likely to contradict each other in stating the same fact ? Do you think that statement of B is always true ?
A and B throw a pair of dice alternatively, till one of them gets a total of 10 and wins the game. Find their respective probabilities of winning, if A starts first.
A die, whose faces are marked 1, 2, 3 in red and 4, 5, 6 in green, is tossed. Let A be the event “number obtained is even” and B be the event “number obtained is red”. Find if A and B are independent events.
Form the differential equation of the family of circles in the second quadrant and touching the co-ordinate axes.
Show that the relation R on the set Z of all integers defined by (x, y) ∈ is divisible by 3 is an equivalence relation.
Find the equation of the tangent to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at point x = 1, y = 0.