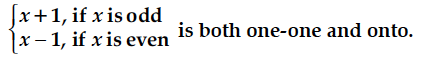Show that a function f : R → R given by f(x) =ax + b,a, b ∈ R, a ≠ 0 is a bijective.
If f : R → R and g : R → R are given by f(x) = sin x and g(x) = 5x² then find gof(x)
If the function f : R → R is given by f(x) = x² + 3x + 1 and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Show that the relation R in the set N × N defined by (a, b) R (c, d) if a² + d² = b² + c² is an equivalence relation.
If the function f : R → R is given by f(x) = and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Is f⁻¹ = g?