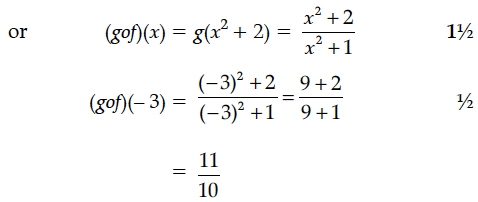
If the function f : R → R is given by f(x) = x² + 3x + 1 and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Let f : R → R be defined by f(x) = 3x² – 5 and g : R → R be defined by g(x) = find gof(x) .
If the function f : R → R is given by f(x) = and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Is f⁻¹ = g?
If the function f : R → R be defined by f(x) = 2x – 3 and g : R → R by g(x) = x³ + 5, then find fog and show that fog is invertible. Also, find (fog)⁻¹, hence find (fog)⁻¹(9).
If f : R → R and g : R → R are given by f(x) = sin x and g(x) = 5x² then find gof(x)
Let f, g : R → R be two functions defined as f (x) = |x| + x and g (x) = |x| – x for all x ∈ R.Then find fog and gof.
If the function f : R → R is given by f(x) = and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Is f⁻¹ = g?
Find the particular solution of the differential equation given that x = 0 when y = 1.
Find the equations of tangents to the curve y = (x²– 1) (x – 2) at the points, where the curve cuts the X-axis.
Find the particular solution of the differential equation given that y = 1, when x = 0.
A bag contains (2n + 1) coins. It is known that (n – 1) of these coins have a head on both sides, whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed. If the probability that the toss results in a head is 31/42, determine the value of n.
Find the angle of intersection of the curves x² + y² = 4 and (x – 2)² + y²= 4, at the point in the first quadrant.