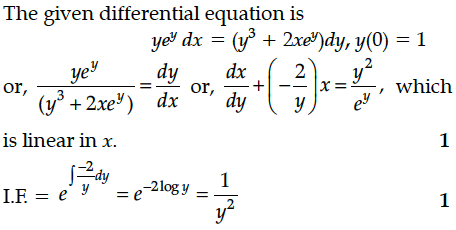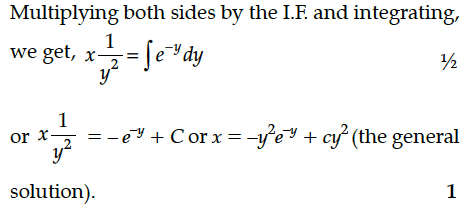Question

Show that the relation S in the set R of real numbers defined as S = {(a, b) : a, b ∈ R and a ≤ b³} is neither reflexive nor symmetric nor transitive.

Find the particular solution of the differential equation : $y e^{y}\,d x=(y^{3}+2x e^{y})d y,y(0)=1$

Find the points on the curve y = x³ – 3x² – 9x + 7 at which the tangent to the curve is parallel to the x-axis.

Let A = R – {2}, B = R – {1}. If f : A → B is a function defined by $f(x)\,=\,\left({\frac{x-1}{x-2}}\right)\!,$ show that f is one-one and onto. Hence find $f^{-1}.$

Let R be a relation defined on the set of natural numbers N as follow : R = {(x, y) : $x\in N,y\in N$ and 2x + y = 24} Find the domain and range of the relation R. Also,find if R is an equivalence relation or not.

For the following matrices A and B, verify that [AB]’ = B’A’ where, A = $\left(\begin{array}{l }1 \\ -4 \\ 3\end{array}\right)$ , B = $\left(\begin{array}{l l l }-1 & 2 & 1\end{array}\right)$

Let $\stackrel{\rightarrow}{a}\$ = $\stackrel{\wedge}{i}+\stackrel{\wedge}{j} +\stackrel{\wedge}{k}$, $\stackrel{\rightarrow}{b}\$ = $4\stackrel{\wedge}{i}-2\stackrel{\wedge}{j} +3\stackrel{\wedge}{k}$ , and $\stackrel{\rightarrow}{c}\$ = $\stackrel{\wedge}{i}-2\stackrel{\wedge}{j} +\stackrel{\wedge}{k}$ Find a vector of magnitude 6 units,which is parallel to the vector $2\stackrel{\rightarrow}{a}-\stackrel{\rightarrow}{b}+3\stackrel{\rightarrow}{c}$.