For the curve y = 4x³ – 2x⁵, find all those points at which the tangent passes through the origin.
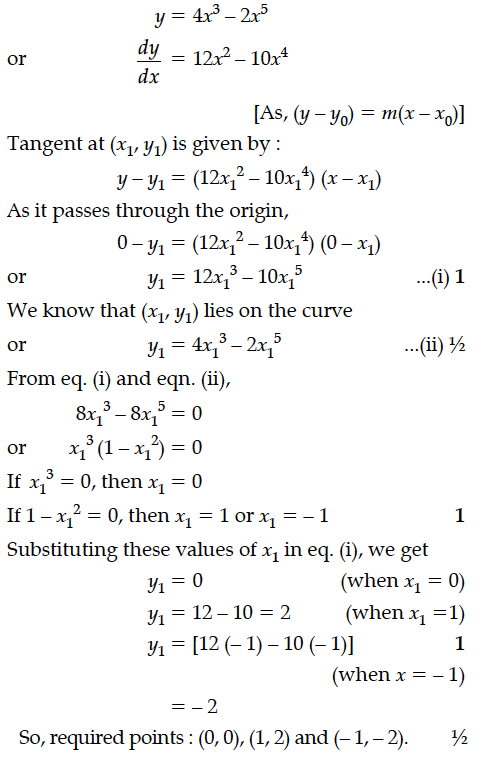
Find the equations of the normal to the curve x² = 4y which passes through the point (1, 2).
Find the point on the curve y = x³ – 11x + 5 at which the equation of tangent is y = x – 11.
Find the points on the curve y = x³ – 3x² – 9x + 7 at which the tangent to the curve is parallel to the x-axis.
Find the points on the curve x² + y² – 2x – 3 = 0 at which tangent is parallel to x-axis.
Find the particular solution of the differential equation given that x = 0 when y = 1.
For the following matrices A and B, verify that [AB]’ = B’A’ where, A = , B =
Find the particular solution of the differential equation : 4x cosec x, (x ≠ 0), given, that y = 0,when
Let A = R – {3}, B = R – {1}. Let f : A → B be defined by f(x) = Show that f is bijective. Also, find
(i) x, if = 4
(ii)
Find the general solution of the following differential equation :
A problem in mathematics is given to 4 students A, B, C, D. Their chances of solving the problem, respectively, are 1/3, 1/4, 1/5 and 2/3. What is the probability that
(i) the problem will be solved ?
(ii) at most one of them solve the problem ?
