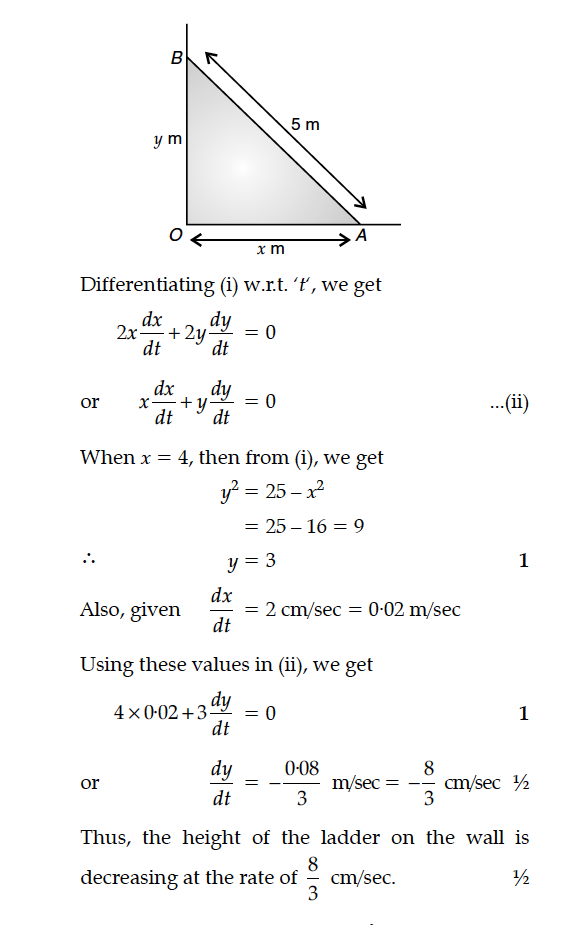
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing, when the foot of the ladder is 4 m away from the wall ?
The side of an equilateral triangle is increasing at the rate of 2 cm/s. At what rate is its area increasing when the side of the triangle is 20 cm ?
The volume of a cube is increasing at the rate of 9 cm³/sec. How fast is the surface area increasing when the length of an edge is 10 cm.
The length x, of a rectangle is decreasing at the rate of 5 cm/minute and the width y, is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rate of change of the area of the rectangle.
The volume of a sphere is increasing at the rate of 8 cm³/sec. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
The radius r of a right circular cone is decreasing at the rate of 3 cm/minute and the height h is increasing at the rate of 2 cm/minute. When r = 9 cm and h = 6 cm, find the rate of change of its volume.
The radius r of a right circular cylinder is increasing at the rate of 5 cm/min and its height h, is decreasing at the rate of 4 cm/min. When r= 8 cm and h = 6 cm, find the rate of change of the volume of cylinder.
For the curve y = 5x – 2x³, if x increases at the rate of 2 units/sec, then find the rate of change of the slope of the curve when x = 3.
The amount of pollution content added in air in a city due to x-diesel vehicles is given by p(x) = 0·005x³ + 0·02x² + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added.
Let f : W → W be defined as show that f is invertible. Find the inverse of f,where W is the set of all whole numbers.
Find the particular solution of the differential equation given that y = 0, when x = 0.
Let f : X -> Y be a function. Define a relation R on X given be R = {(a, b) : f(a) = f(b)}. Show that R is an equivalence relation ?
Let f : N → R be a function defined as f(x) = 4x² + 12x + 15. Then show that f : N → S, where S is range of f, is invertible. Also find the inverse of f.
