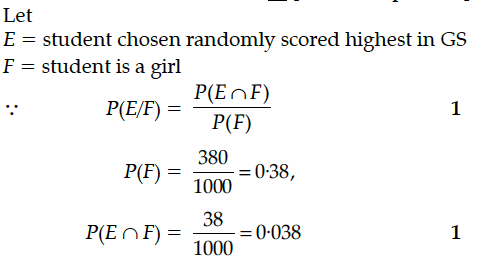
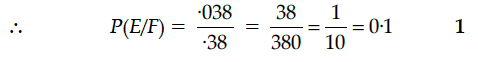
A box contains 50 bolts and 50 nuts. Half of the bolts and nuts are rusted. If two items are drawn with replacement, what is the probability that either both are rusted or both are bolts.
P speaks truth in 70% of the cases and Q in 80% of the cases. In what percent of cases are they likely to agree
in stating the same fact ?
Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls ? Given that :
(i) the youngest is a girl.
(ii) atleast one is a girl.
A and B throw a pair of dice alternately. A wins the game if he gets a total of 7 and B wins the game if he gets a total of 10. If A starts the game, then find the probability that B wins.
If A and B are two independent events, then prove that the probability of occurrence of at least one of A and B is given by 1 – P(A’) · P(B’)
A and B throw a pair of dice alternatively, till one of them gets a total of 10 and wins the game. Find their respective probabilities of winning, if A starts first.
A couple has 2 children. Find the probability that both are boys, if it is known that
(i) one of them is a boy
(ii) the older child is a boy.
A speaks truth in 75% of the cases, while B in 90% of the cases. In what percent of cases are they likely to contradict each other in stating the same fact ? Do you think that statement of B is always true ?
Probability of solving specific problem independently by A and B are 1/2 and 1/3 respectively. If both try to solve the problem, independently, then find the probability that
(i) the problem is solved
(ii) exactly one of them solves the problem
Find the particular solution of the following differential equation given that at x = 2, y = 1
If the function f : R → R be given by f(x) = x² + 2 and g : R → R be given by g(x) = find fog and gof and hence find fog(2) and gof(– 3).
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing, when the foot of the ladder is 4 m away from the wall ?
Form the differential equation representing family of curves given by (x – a)² + 2y²= a², where a is an arbitrary constant.