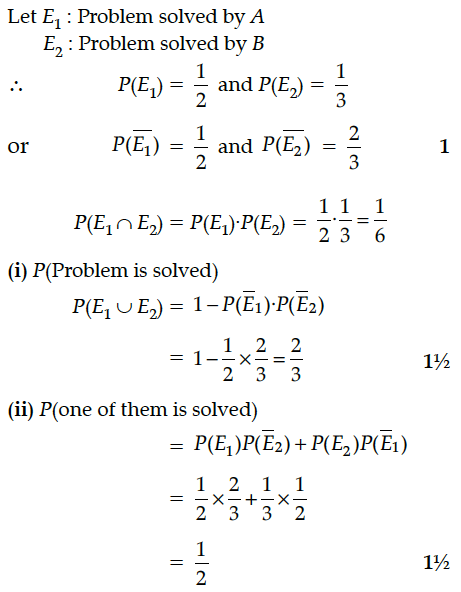
A problem in mathematics is given to 4 students A, B, C, D. Their chances of solving the problem, respectively, are 1/3, 1/4, 1/5 and 2/3. What is the probability that
(i) the problem will be solved ?
(ii) at most one of them solve the problem ?
A box contains 50 bolts and 50 nuts. Half of the bolts and nuts are rusted. If two items are drawn with replacement, what is the probability that either both are rusted or both are bolts.
A couple has 2 children. Find the probability that both are boys, if it is known that
(i) one of them is a boy
(ii) the older child is a boy.
If E and F are independent events, then show that
(i) E and F' are independent events.
(ii) E' and F are also independent events.
Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls ? Given that :
(i) the youngest is a girl.
(ii) atleast one is a girl.
P speaks truth in 70% of the cases and Q in 80% of the cases. In what percent of cases are they likely to agree
in stating the same fact ?
A and B throw a pair of dice alternatively, till one of them gets a total of 10 and wins the game. Find their respective probabilities of winning, if A starts first.
Three schools A, B and C organised a fete (mela) collecting funds for flood victims in which they sold hand-helds fans, mats and toys made from recycled material, the sale price of each being ₹ 25, ₹ 100 and ₹ 50 respectively. The following table shows the number of articles of each type sold :
Let A = R – {2}, B = R – {1}. If f : A → B is a function defined by show that f is one-one and onto. Hence find
A and B throw a pair of dice alternately. A wins the game if he gets a total of 9 and B wins if he gets a total of 7. If A starts the game, find the probability of winning the game by B.
Find the points on the curve x² + y² – 2x – 3 = 0 at which tangent is parallel to x-axis.
A trust fund has ₹ 35,000 is to be invested in two different types of bonds. The first bond pays 8% interest per annum which will be given to orphanage and second bond pays 10% interest per annum which will be given to an N.G.O. (Cancer Aid Society). Use matrix multiplication, determine how to divide ₹ 35,000 among two types of bonds if the trust fund obtains an annual total interest of ₹ 3,200.
Find the angle of intersection of the curves x² + y² = 4 and (x – 2)² + y²= 4, at the point in the first quadrant.