Write the differential equation formed from the equation y = mx + c, where m and c are arbitrary constants.
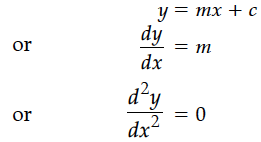
From the differential equation of equation y = a cos 2x + b sin 2x, where a and b are constant.
Find the differential equation representing the family of curves where A and B are arbitrary constants.
Form the differential equation of all circles which is tough the x-axis at the origin.
Form the differential equation representing family of curves given by (x – a)² + 2y²= a², where a is an arbitrary constant.
Let R be the equivalence relation in the set A = {0, 1, 2, 3, 4, 5} given by R = {(a, b) : 2 divides (a –b)}. Write the equivalence class [0].
