Find the sum of the order and the degree of the following differential equations :
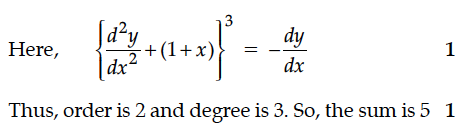
Find the particular solution of the following differential equation :
y = 0 when x = 0.
The volume of a sphere is increasing at the rate of 8 cm³/sec. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
The radius r of a right circular cylinder is decreasing at the rate of 3 cm/min. and its height h is increasing at the rate of 2 cm/min. When r =7 cm and h = 2 cm, find the rate of change of the volume of cylinder.
If P(F) = 0·35 and P(E U F) = 0·85 and E and F are independent events. Find P(E).
The volume of a cube is increasing at the rate of 9 cm³/sec. How fast is the surface area increasing when the length of an edge is 10 cm.
If A and B are two independent events, then prove that the probability of occurrence of at least one of A and B is given by 1 – P(A’) · P(B’)
Show that the function f(x) = x³ – 3x² + 6x – 100 is increasing on R.
