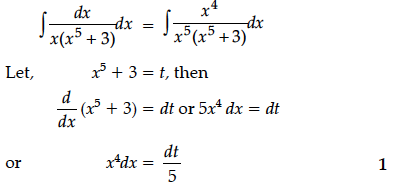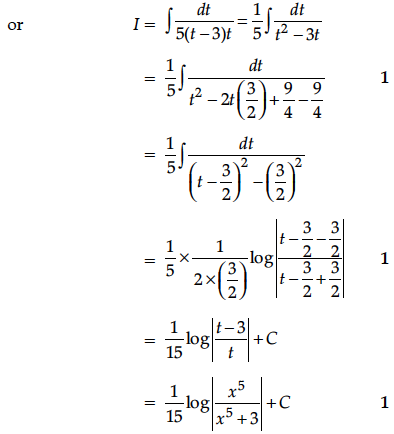Question

Let A = {1, 2, 3, . ...., 9} and R be the relation in A × A defined by (a, b) R (c, d) if a + d =b + c for (a, b), (c, d) in A × A. Prove that R is an equivalence relation. Also obtain the equivalence class [(2, 5)].

The side of an equilateral triangle is increasing at the rate of 2 cm/s. At what rate is its area increasing when the side of the triangle is 20 cm ?

Find : $\large\textstyle\int$$\large{\frac{x}{(x^{2}+1)(x-1)}}\,d x.$

A problem in mathematics is given to 4 students A, B, C, D. Their chances of solving the problem, respectively, are 1/3, 1/4, 1/5 and 2/3. What is the probability that (i) the problem will be solved ? (ii) at most one of them solve the problem ?

Find the approximate value of f(3·02), up to 2 places of decimal, where f(x) = 3x² + 5x + 3.

Find the particular solution of the differential equation : ${\frac{d y}{d x}}\ +y\;{\cot{x}}=$ 4x cosec x, (x ≠ 0), given, that y = 0,when $x={\frac{\pi}{2}}$

Evaluate : $\large\textstyle\int$$\large{\frac{x}{(x-1)^{2}(x+2)}}d x\ .$