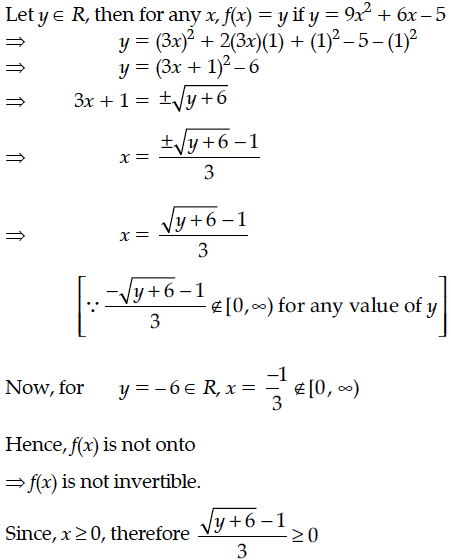
If the function f : R → R is given by f(x) = x² + 3x + 1 and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Show that a function f : R → R given by f(x) =ax + b,a, b ∈ R, a ≠ 0 is a bijective.
Show that the function f : R {x ∈ R – 1 < x < 1} defined by f(x) = x ∈ R is one-one and onto function. Hence find f⁻¹(x).
Show that f : N → N, given by f(x) = |``x+1, if x is odd x- 1, if x is even is both one-one and onto.``|
If the function f : R → R be given by f(x) = x² + 2 and g : R → R be given by g(x) = find fog and gof and hence find fog(2) and gof(– 3).
If the function f : R → R be defined by f(x) = 2x – 3 and g : R → R by g(x) = x³ + 5, then find fog and show that fog is invertible. Also, find (fog)⁻¹, hence find (fog)⁻¹(9).
To promote the making of toilets for women, as organisation tried to generate awareness through (i) house calls (ii) letters and (iii) announcements.
The cost for each mode per attempt is given below :
(i) ₹ 50 (ii) ₹ 20 (iii) ₹ 40
The number of attempts made in three villages X, Y and Z and given below :
Two farmers X and Y cultivate only three varieties of rice namely Basmati, Permal and Naura. The sale in rupees of these varieties of rice by both the farmers in the months of September and October are given by the following matrices A and B.
Solve the differential equation + given that y = 1 when x = 1.
If the function f : R → R be defined by f(x) = 2x – 3 and g : R → R by g(x) = x³ + 5, then find fog and show that fog is invertible. Also, find (fog)⁻¹, hence find (fog)⁻¹(9).