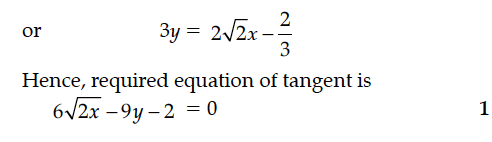Question

Using properties of determinants, prove that : $\begin{vmatrix}b+c & c+a & a+b \\ q+r & r+p & p+q \\ y+z & z+x & x+y\end{vmatrix}$ = 2 $\begin{vmatrix}a & b & c \\ p & q & r \\ x & y & z\end{vmatrix}$ .

Evaluate : ($\large\textstyle\int(3x-2){\sqrt{x^{2}+x+1}}\,d x~.$

Let A = R – {2}, B = R – {1}. If f : A → B is a function defined by $f(x)\,=\,\left({\frac{x-1}{x-2}}\right)\!,$ show that f is one-one and onto. Hence find $f^{-1}.$

Sand is pouring from the pipe at the rate of 12 cm³/s. The falling sand forms a cone on a ground in such a way that the height of cone is always one-sixth of radius of the base. How fast is the height of sand cone increasing when the height is 4 cm ?

Without expanding the determinant at any stage; prove that : $\begin{vmatrix}0 & 2 & -3 \\ -2 & 0 & 4 \\ 3 & -4 & 0\end{vmatrix}$ = 0.

Find the particular solution of the following differential equation : $(x\ +1){\frac{d y}{d x}}=2e^{-y}-1;$ y = 0 when x = 0.

Evaluate : $\large\textstyle\int\!{\frac{\ d x}{x(x^{5}+3)}}\,.$