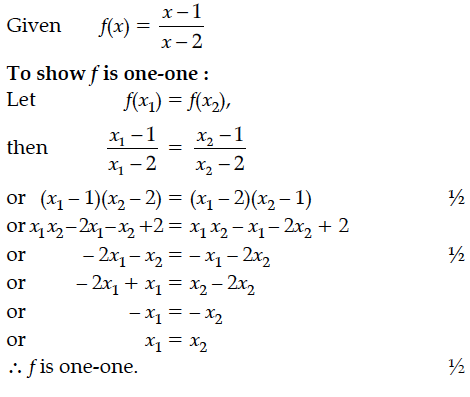
Let A = R – {3}, B = R – {1}. Let f : A → B be defined by f(x) = Show that f is bijective. Also, find
(i) x, if = 4
(ii)
Show that the function f : R {x ∈ R – 1 < x < 1} defined by f(x) = x ∈ R is one-one and onto function. Hence find f⁻¹(x).
Find the particular solution of the following differential equation :
y = 0, when x = 2.
The total expenditure (in ₹) required for providing the cheap edition of a book for poor and deserving students is given by R(x) = 3x² + 36x, where x is the number of set of books. If the marginal expenditure is defined as write the marginal expenditure required for 1200 such sets.
The equation of tangent at (2, 3) on the curve y² = ax³ + b is y = 4x – 5. Find the values of a and b.
Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls ? Given that :
(i) the youngest is a girl.
(ii) atleast one is a girl.
The side of an equilateral triangle is increasing at the rate of 2 cm/s. At what rate is its area increasing when the side of the triangle is 20 cm ?