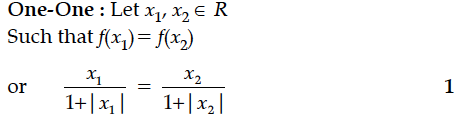
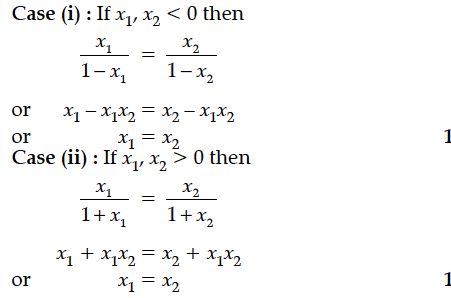
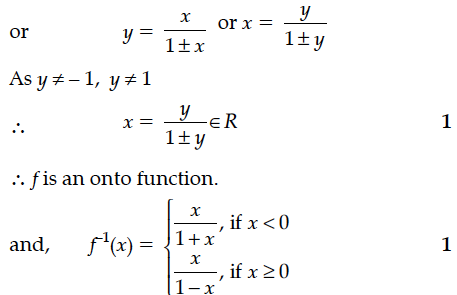
Show that a function f : R → R given by f(x) =ax + b,a, b ∈ R, a ≠ 0 is a bijective.
Show that the relation R on the set Z of all integers defined by (x, y) ∈ is divisible by 3 is an equivalence relation.
Let A = R – {2}, B = R – {1}. If f : A → B is a function defined by show that f is one-one and onto. Hence find
Find the equation of the tangent line to the curve y =x² -2x + 7 which is
(i) parallel to the line 2x-y +9 =0
(ii) perpendicular to the line 5y - 15x = 13.
In a hockey match, both teams A and B scored same number of goals up to the end of the game, so to decide the winner, the referee asked both the captains to throw a die alternately and decided that the team, whose captain gets a six first, will be declared the winner. If the captain of team A was asked to start, find their respective probabilities of winning the match and state whether the decision of the referee was fair or not.
Obtain the differential equation of all the circles of radius r.
Find the equations of tangents to the curve 3x² – y² = 8, which passes through the point
Solve the differential equation x cos x + sin x, given that y = 1 when
Find the equation of the normal at a point on the curve x² = 4y which passes through the point (1, 2). Also find the equation of the corresponding tangent.