The temperature coefficient of resistivity, for two materials A and B, are 0.0031 / °C and 0.0068 / °C respectively.
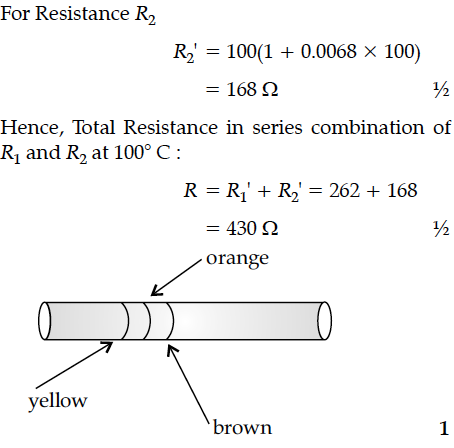
Two resistors R1 and R2, made from materials A and B, respectively, have resistances of 200 Ω and 100 Ω at 0°C. Show on a diagram, the 'colour code', of a carbon resistor, that would have a resistance
equal to the series combination of R1 and R2, at a temperature of 100°C.
(Neglect the ring corresponding to the tolerance of the carbon resistor).
Two resistors R1 and R2, made from materials A and B, respectively, have resistances of 200 Ω and 100 Ω at 0°C. Show on a diagram, the 'colour code', of a carbon resistor, that would have a resistance
equal to the series combination of R1 and R2, at a temperature of 100°C.
(Neglect the ring corresponding to the tolerance of the carbon resistor).

A student connects a cell, of emf E2 and internal resistance r2 with a cell of emf E1 and internal resistance r1, such that their combination has a net internal resistance less than r1. This combination is then connected across a resistance R. Draw a diagram of the 'set-up' and obtain an expression for the current flowing through the resistance.
First a set of n equal resistors of R each is connected in series to a battery of emf E and internal resistance R. A current I is observed to flow. Then the n resistors are connected in parallel to the same battery. It is observed that the current becomes 10 times. What is n ?
A resistance of R Ω draws current from a potentiometer. The potentiometer has a total resistance \(R_0\) Ω as shown in the Fig below. A voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of the potentiometer.
A battery of emf E and internal resistance, r, when connected with an external resistance of 12Ω produces a current of 0.5 A. When connected across a resistance of 25Ω, it produces a current of 0.25 A. Determine
(i) the emf and (ii) the internal resistance of the cell.
Two metallic wires P₁ and P₂ of the same material and same length but different cross-sectional areas A₁ and A₂ are joined together and then connected to a source of emf. Find the ratio of the drift velocities of free electrons in the wires P₁ and P₂ if the wires are connected
(i) in series, and (ii) in parallel.
Derive the expression for the current density of a conductor in terms of the conductivity and applied electric field. Explain, with reason how the mobility of electrons in a conductor changes when the potential difference applied is doubled, keeping the temperature of the conductor constant.
(a) Define the term ‘conductivity’ of a metallic wire. Write its SI unit.
(b) Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in terms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E.
(i) A point charge (+Q) is kept in the vicinity of an uncharged conducting plate. Sketch electric field lines between the charge and the plate.
(ii) Two infinitely large plane thin parallel sheets having surface charge densities σ₁ and σ₂ (σ₁ > σ₂) are shown in the figure. Write the magnitudes and directions of the fields in the regions marked II and III.
A sinusoidal voltage of peak value 10 V is applied to a series LCR circuit in which resistance,capacitance and inductance have values of 10 Ω,1 µF and 1 H respectively. Find
(i) the peak voltage across the inductor at resonance
(ii) quality factor of the circuit.
Define the term current density of a metallic conductor. Deduce the relation connecting current density (J) and the conductivity σ of the conductor, when an electric field E, is applied to it.
Define an equipotential surface. Draw equipotential surfaces :
(i) in the case of a single point charge and
(ii) in a constant electric field in z-direction. Why the equipotential surfaces about a single charge are not equidistant ?
(iii) Can electric field exist tangential to an equipotential surface ? Give reason.
A charge is distributed uniformly over a ring of radius ‘a’. Obtain an expression for the electric intensity E at a point on the axis of the ring. Hence, show that for points at large distances from the ring, it behaves like a point charge.
Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons ? Use this relation to deduce the expression for the electrical resistivity of the material.
The potential difference across a resistor ‘r’ carrying current ‘I’ is Ir.
(i) Now if the potential difference across ‘r’ is measured using a voltmeter of resistance ‘’, show that the reading of voltmeter is less than the true value.
(ii) Find the percentage error in measuring the potential difference by a voltmeter.
(iii) At what value of ’, does the voltmeter measures the true potential difference?
