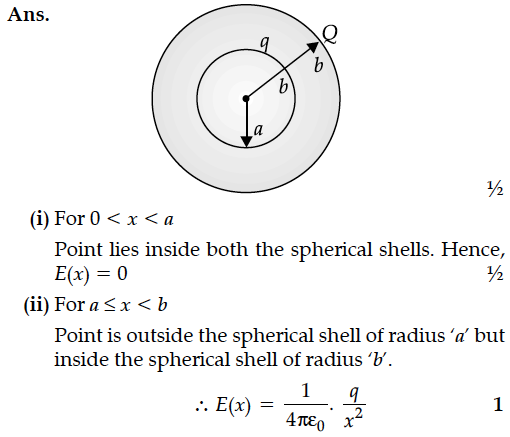
Two thin concentric and coplanar spherical shells, of radii a and b (b > a) carry charges, q and Q, respectively. Find the magnitude of the electric field, at a point at distance x, from their common centre for :
(i) 0 < x < a
(ii) a x < b
(iii) b x <
(i) 0 < x < a
(ii) a x < b
(iii) b x <
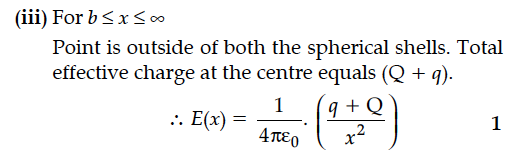
Two point charges q1 and q2 are located at points (a, 0, 0) and (0, b, 0) respectively. Find the electric field due to both these charges at the point (0, 0, c).
A charge + Q, is uniformly distributed within a sphere of radius R. Find the electric field, due to this charge distribution, at a distant point r from the centre of the sphere where :
(i) 0 < r < R
(ii) r > R
A charge Q is enclosed by a Gaussian spherical surface of radius R. If the radius is doubled, then the outward electric flux will
(A) Increase four times
(B) be reduced to half
(C) remain the same
(D) Be doubled
(i) Derive the expression for electric field at a point on the equatorial line of an electric dipole.
(ii) Depict the orientation of the dipole in (i) stable, (ii) unstable equilibrium in a uniform electric field.
The given figure shows tracks of three charged particles in a uniform electrostatic field. Which of them is probably an α-particle?
(A) 1
(B) 2
(C) 3
(D) None of the above
Two dipoles, made from charges ± q and ± Q respectively, have equal dipole moments. Give the
(i) ratio between the ‘separations’ of these two pairs of charges,
(ii) angle between the dipole axes of these two dipoles.
Two-point charges 2μC and 4μC are placed 2 cm apart. The ratio of the Coulomb’s force experienced by them is
(A) 1: 2
(B) 2: 1
(C) 1: 1
(D) 4: 1
(i) Write two properties by which electric potential is related to the electric field.
(ii) Two point charges q₁ and q₂ separated by a distance of r₁₂ are kept in an external electric field. Derive an expression for the potential energy of the system of two charges in the field.
Define the term current density of a metallic conductor. Deduce the relation connecting current density (J) and the conductivity σ of the conductor, when an electric field E, is applied to it.
An electric dipole is placed in a uniform electric field.
(i) Show that no translatory force acts on it.
(ii) Derive an expression for the torque acting on it.
(iii) Find work done in rotating the dipole through 180°.
A charge is distributed uniformly over a ring of radius ‘a’. Obtain an expression for the electric intensity E at a point on the axis of the ring. Hence, show that for points at large distances from the ring, it behaves like a point charge.
(i) A point charge (+Q) is kept in the vicinity of an uncharged conducting plate. Sketch electric field lines between the charge and the plate.
(ii) Two infinitely large plane thin parallel sheets having surface charge densities σ₁ and σ₂ (σ₁ > σ₂) are shown in the figure. Write the magnitudes and directions of the fields in the regions marked II and III.
The temperature coefficient of resistivity, for two materials A and B, are 0.0031 / °C and 0.0068 / °C respectively.
Two resistors R1 and R2, made from materials A and B, respectively, have resistances of 200 Ω and 100 Ω at 0°C. Show on a diagram, the 'colour code', of a carbon resistor, that would have a resistance
equal to the series combination of R1 and R2, at a temperature of 100°C.
(Neglect the ring corresponding to the tolerance of the carbon resistor).
A student connects a cell, of emf E2 and internal resistance r2 with a cell of emf E1 and internal resistance r1, such that their combination has a net internal resistance less than r1. This combination is then connected across a resistance R. Draw a diagram of the 'set-up' and obtain an expression for the current flowing through the resistance.
