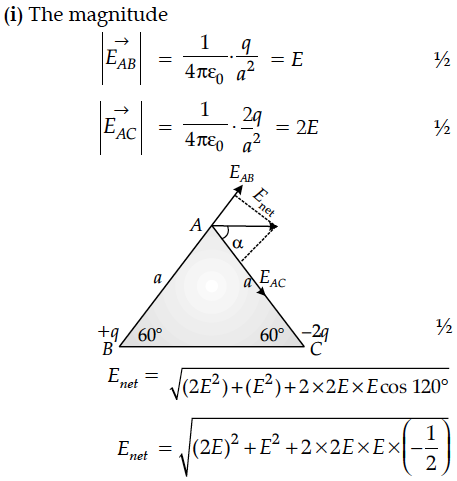
Two point charges + q and –2q are placed at the vertices ‘B’ and ‘C’ of an equilateral triangle ABC of side ‘a‘ as given in the figure. Obtain the expression for (i) the magnitude and (ii) the direction of the resultant electric field at the vertex A due to these two charges.


Five charges, q each are placed at the corners of a regular pentagon of side a.
(i) What will be the electric field at O if the charge from one of the corners (say A) is removed ?
(ii) What will be the electric field at O if the charge q at A is replaced by - q ?
Two point charges ‘q1’ and ‘q2’ are placed at a distance ‘d’ apart as shown in the figure. The electric field intensity is zero at a point ‘P’ on the line joining them as shown. Write two conclusions that you can draw from this.
Three charges each equal to 2 μC are placed at the corners of an equilateral triangle. If force between any two charges is 2F, then the net force on either will be:
Two point charges q1 and q2 are located at points (a, 0, 0) and (0, b, 0) respectively. Find the electric field due to both these charges at the point (0, 0, c).
A point charge +Q is placed in the vicinity of a conducting surface. Draw the electric field lines between the surface and the charge.
Two equal balls having equal positive charge ‘q’ coulombs are suspended by two insulating strings of equal length. What would be the effect on the force when a plastic sheet is inserted between the two ?
Two charges q and –3q are placed on x-axis separated by distance d. Where a third charge 2q should be placed such that it will not experience any force ?
A particle, having a charge +5 µC, is initially at rest at the point x = 30 cm on the x-axis. The particle begins to move due to the presence of a charge Q that is kept fixed at the origin. Find the kinetic energy of the particle at the instant it has moved 15 cm from its initial position if
(a) Q = +15 µC and
(b) Q = – 15 µC
(i) Deduce the relation between current I flowing through a conductor and drift velocity of the electrons.
(ii) Figure shows a plot of current ‘I’ flowing through the cross-section of a wire versus the time ‘t’. Use the plot to find the charge flowing in 10 s through the wire.
A circuit containing an 80 mH inductor and a 250 µF capacitor in series connected to a 240 V,100 rad/s supply. The resistance of the circuit is negligible.
(i) Obtain rms value of current.
(ii) What is the total average power consumed by the circuit ?
(i) Derive the expression for the electric potential due to an electric dipole at a point on its axial line.
(ii) Depict the equipotential surface due to electric dipole.
Obtain the expression for the energy density of magnitude field B produced in the inductor.
Two thin concentric and coplanar spherical shells, of radii a and b (b > a) carry charges, q and Q, respectively. Find the magnitude of the electric field, at a point at distance x, from their common centre for :
(i) 0 < x < a
(ii) a x < b
(iii) b x <
(i) Derive an expression for drift velocity of electrons in a conductor. Hence deduce Ohm’s law.
(ii) A wire whose cross-sectional area is increasing linearly from its one end to the other, is connected across a battery of V volts. Which of the following quantities remain constant in the wire ?
(a) drift speed
(b) current density
(c) electric current
(d) electric field
Justify your answer.
