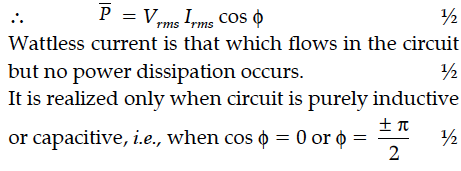
A sinusoidal voltage of peak value 10 V is applied to a series LCR circuit in which resistance,capacitance and inductance have values of 10 Ω,1 µF and 1 H respectively. Find
(i) the peak voltage across the inductor at resonance
(ii) quality factor of the circuit.
A voltage V = V₀ sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipate over a cycle.Under what conditions is
(i) no power dissipated even though the current flows through the circuit,
(ii)maximum power dissipated in the circuit ?
Show that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and the inductor is constant in time.
In a series LCR circuit, obtain the conditions under which
(i) the impedance of the circuit is minimum, and
(ii) wattless current flows in the circuit.
An alternating voltage given by V = 140sin314 t is connected across a pure resistor of 50 Find :
(i) the frequency of the source.
(ii) the rms current through the resistor.
An ac voltage V = V₀ sin ωt is applied to a pure inductor L. Obtain an expression for the current in the circuit. Prove that the average power supplied to an inductor over one complete cycle is zero.
A lamp is connected in series with a capacitor. Predict your observation for dc and ac connections. What happens in each if the capacitance of the capacitor is reduced ?
(i) Write two properties by which electric potential is related to the electric field.
(ii) Two point charges q₁ and q₂ separated by a distance of r₁₂ are kept in an external electric field. Derive an expression for the potential energy of the system of two charges in the field.
A voltage V = V₀ sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipate over a cycle.Under what conditions is
(i) no power dissipated even though the current flows through the circuit,
(ii)maximum power dissipated in the circuit ?
What is relaxation time ? Derive an expression for resistivity of a wire in terms of number density of free electrons and relaxation time.
Two cells of emfs E₁ & E₂ and internal resistances r₁ & r₂ respectively are connected in parallel. Obtain expressions for the equivalent.
(i) resistance and
(ii) emf of the combination
An inductor of 200 mH, capacitor of 400 µF and a resistor of 10 Ω are connected in series to ac source of 50 V of variable frequency. Calculate the
(a) angular frequency at which maximum power dissipation occurs in the circuit and the corresponding value of the effective current, and
(b) value of Q-factor in the circuit.
(i) Deduce the relation between current I flowing through a conductor and drift velocity of the electrons.
(ii) Figure shows a plot of current ‘I’ flowing through the cross-section of a wire versus the time ‘t’. Use the plot to find the charge flowing in 10 s through the wire.
Define the term current density of a metallic conductor. Deduce the relation connecting current density (J) and the conductivity σ of the conductor, when an electric field E, is applied to it.