To promote the making of toilets for women, as organisation tried to generate awareness through (i) house calls (ii) letters and (iii) announcements.
The cost for each mode per attempt is given below :
(i) ₹ 50 (ii) ₹ 20 (iii) ₹ 40
The number of attempts made in three villages X, Y and Z and given below :
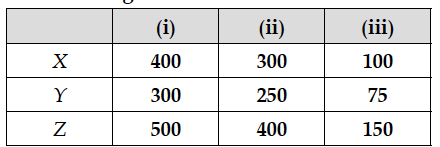
Find the total cost incurred by the organisation for the three villages separately, using matrices.
The cost for each mode per attempt is given below :
(i) ₹ 50 (ii) ₹ 20 (iii) ₹ 40
The number of attempts made in three villages X, Y and Z and given below :

Find the total cost incurred by the organisation for the three villages separately, using matrices.


In a parliament election, a political party hired a public relations firm to promote its candidates in three ways — telephone, house calls and letters. The cost per contact (in paise) is given in matrix A as
A trust fund has ₹ 35,000 is to be invested in two different types of bonds. The first bond pays 8% interest per annum which will be given to orphanage and second bond pays 10% interest per annum which will be given to an N.G.O. (Cancer Aid Society). Use matrix multiplication, determine how to divide ₹ 35,000 among two types of bonds if the trust fund obtains an annual total interest of ₹ 3,200.
A bag contains (2n + 1) coins. It is known that (n – 1) of these coins have a head on both sides, whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed. If the probability that the toss results in a head is 31/42, determine the value of n.
Let A = R – {2}, B = R – {1}. If f : A → B is a function defined by show that f is one-one and onto. Hence find
If f(x) = then Show that fof(x) = x for all What is the inverse of f?
Find the equations of the normal to the curve x² = 4y which passes through the point (1, 2).
Prove that the function f : [0, ∞) → R given by f(x) = 9x² + 6x – 5 is not invertible. Modify the Codomain of the function f to make it invertible, and hence find f⁻¹.
Solve the differential equation = 2 cos x, given that y = 0 when
Solve the following differential equation. (1 + y²) (1 + log |x|) dx + x dy = 0
