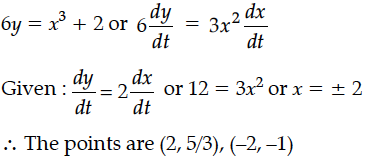
Find the points on the curve y = x³ at which the slope of the tangent is equal to y-coordinate of the point.
Find the slope of tangent to the curve y = 3x² – 6 at the point on it whose x-coordinate is 2.
Find the point on the curve y = x³ – 11x + 5 at which the equation of tangent is y = x – 11.
Find the points on the curve x² + y² – 2x – 3 = 0 at which tangent is parallel to x-axis.
Find the points on the curve y = x³ – 3x² – 9x + 7 at which the tangent to the curve is parallel to the x-axis.
For the curve y = 4x³ – 2x⁵, find all those points at which the tangent passes through the origin.
The radius r of a right circular cylinder is increasing uniformly at the rate of 0.3 cm/s and its height h is decreasing at the rate of 0.4 cm/s. When r = 3.5 cm and h = 7 cm, find the rate of change of the curved surface area of the cylinder.
For the curve y = 5x – 2x³, if x increases at the rate of 2 units/sec, then find the rate of change of the slope of the curve when x = 3.
A couple has 2 children. Find the probability that both are boys, if it is known that
(i) one of them is a boy
(ii) the older child is a boy.
The position vectors of points A, B and C are , and respectively. If C divides the line segment joining A and B in the ratio 3 : 1, find the values of λ and μ.
The volume of a sphere is increasing at the rate of 8 cm³/sec. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
Obtain the differential equation of the family of circles passing through the points (a, 0) and (– a, 0).