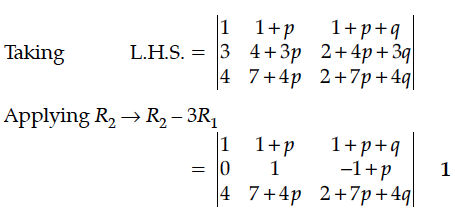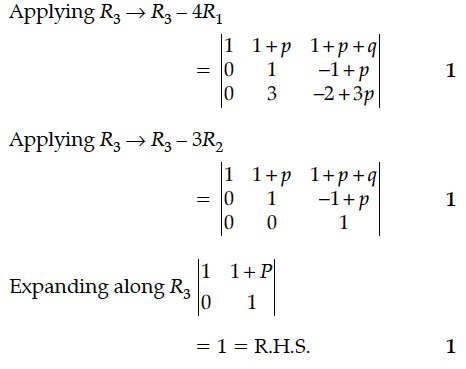Question

Find the particular solution of the differential equation $(1+e^{2x})d y+(1+y^{2})e^{x}d x=0,$ given that y = 1, when x = 0.

Evaluate : $\large\textstyle\int\!{\frac{3x+1}{(x+1)^{2}(x+3)}}d x~.$

Let f : W → W be defined as $f(n)={\binom{n+1,{\mathrm{if~}}~n{\mathrm{~is~even}}}{n-1,{\mathrm{~if~}}~n{\mathrm{~is~odd}}}}$ show that f is invertible. Find the inverse of f,where W is the set of all whole numbers.

Find the particular solution of the differential equation ${\frac{d y}{d x}}\ =1+x+y+x y$ given that y = 0 when x = 1.

Find the equation of tangent to the curve y = cos (x + y), -2π ≤ x ≤ 0, that is parallel to the line x + 2y = 0.

A speaks truth in 75% of the cases, while B in 90% of the cases. In what percent of cases are they likely to contradict each other in stating the same fact ? Do you think that statement of B is always true ?

Find the equations of the tangent and the normal, to the curve 16x² + 9y² = 145 at the point $(x_{1},\;y_{1}),$ where x₁ = 2 and y₁ > 0.