Write the differential equation obtained by eliminating the arbitrary constant C in the equation representing the family of curves xy = C cos x.
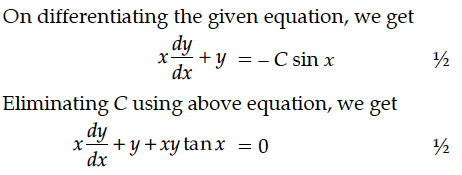
Write the differential equation formed from the equation y = mx + c, where m and c are arbitrary constants.
Form the differential equation of the family of circles in the second quadrant and touching the co-ordinate axes.
From the differential equation of equation y = a cos 2x + b sin 2x, where a and b are constant.
Obtain the differential equation of the family of circles passing through the points (a, 0) and (– a, 0).
Form the differential equation of all circles which is tough the x-axis at the origin.
If A is an invertible square matrix of order 3 and |A| = 5, then find the value of |adj A|.
