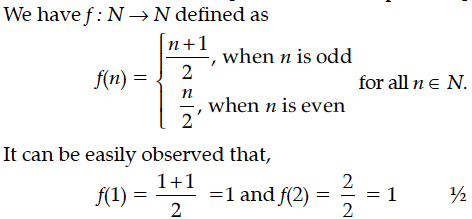
Let f : W → W be defined as show that f is invertible. Find the inverse of f,where W is the set of all whole numbers.
Let R be a relation defined on the set of natural numbers N as follow :
R = {(x, y) : and 2x + y = 24}
Find the domain and range of the relation R. Also,find if R is an equivalence relation or not.
Let f : N → R be a function defined as f(x) = 4x² + 12x + 15. Then show that f : N → S, where S is range of f, is invertible. Also find the inverse of f.
How many equivalence relations on the set {1, 2, 3} containing (1, 2) and (2, 1) are there in all ?Justify your answer.
Consider given by f(x) = 5x² + 6x – 9.Prove that f is invertible with f⁻¹(y) = [where, R⁺ is the set of all nonnegative real numbers.]
Find the particular solution of the differential equation x (1 + y²) dx – y (1 + x²) dy = 0, given that y = 1, when x =0.
Find the particular solution of the differential equation : x ≠ 0. Given that y = 0, when
Find the equations of the normal to the curve y = 4x³ – 3x + 5 which are perpendicular to the line 9x – y + 5 = 0..
Find the general solution of the following differential equation :