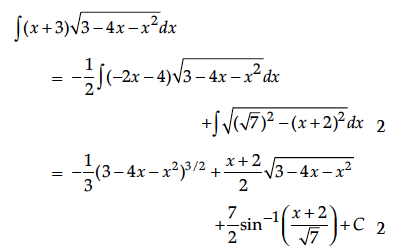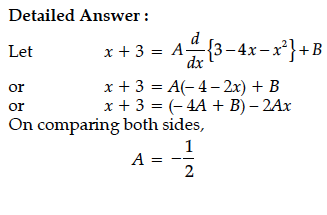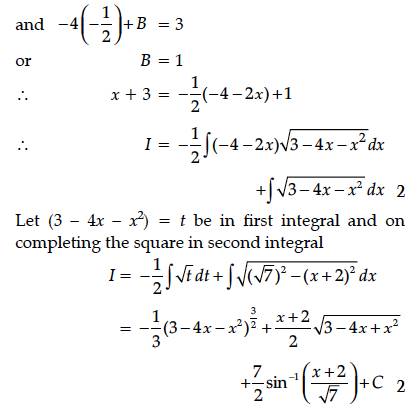Question

Let f, g : R → R be two functions defined as f (x) = |x| + x and g (x) = |x| – x for all x ∈ R.Then find fog and gof.

Let A = R – {2}, B = R – {1}. If f : A → B is a function defined by $f(x)\,=\,\left({\frac{x-1}{x-2}}\right)\!,$ show that f is one-one and onto. Hence find $f^{-1}.$

Find the general solution of the differential equation: ${\frac{d x}{d y}}\;=\;{\frac{y\tan y-x\tan y-x y}{y\tan y}}$

Consider f :$R_{+}\to[4,\infty)$ given by f(x) = x² + 4 Show that f is invertible with the inverse $f^{-1}$ of f given by $f^{-1}(y)$ = $\sqrt{y-4}$ , where $\textstyle R_{+}$ is the set of all nonnegative real numbers.

If A = $\left(\begin{array}{l l l }2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0\end{array}\right)$ , then find value of A² - 3A + 2I.

A speaks truth in 60% of the cases, while B in 90% of cases. In what percent of cases are they likely to contradict each other in stating the same fact ? In the cases of contradiction do you think, the statement of B will carry more weight as he speaks truth in more number of cases than A ?

Let $\stackrel{\rightarrow}{a}\$ = $\stackrel{\wedge}{i}+\stackrel{\wedge}{j} +\stackrel{\wedge}{k}$, $\stackrel{\rightarrow}{b}\$ = $4\stackrel{\wedge}{i}-2\stackrel{\wedge}{j} +3\stackrel{\wedge}{k}$ , and $\stackrel{\rightarrow}{c}\$ = $\stackrel{\wedge}{i}-2\stackrel{\wedge}{j} +\stackrel{\wedge}{k}$ Find a vector of magnitude 6 units,which is parallel to the vector $2\stackrel{\rightarrow}{a}-\stackrel{\rightarrow}{b}+3\stackrel{\rightarrow}{c}$.