A and B throw a pair of dice alternately. A wins the game if he gets a total of 9 and B wins if he gets a total of 7. If A starts the game, find the probability of winning the game by B.
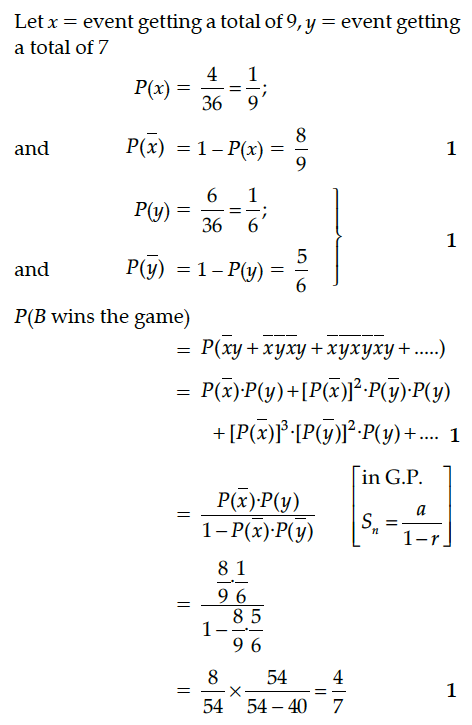
A and B throw a pair of dice alternately. A wins the game if he gets a total of 7 and B wins the game if he gets a total of 10. If A starts the game, then find the probability that B wins.
A and B throw a pair of dice alternatively, till one of them gets a total of 10 and wins the game. Find their respective probabilities of winning, if A starts first.
P speaks truth in 70% of the cases and Q in 80% of the cases. In what percent of cases are they likely to agree
in stating the same fact ?
A couple has 2 children. Find the probability that both are boys, if it is known that
(i) one of them is a boy
(ii) the older child is a boy.
If E and F are independent events, then show that
(i) E and F' are independent events.
(ii) E' and F are also independent events.
If A and B are two independent events, then prove that the probability of occurrence of at least one of A and B is given by 1 – P(A’) · P(B’)
If P(A) = 0.4, P(B) = p, P(A U B) = 0.6 and A and B are given to the independent events, find the value of ‘p’.
Find the equations of the tangent and normal to the curve at the point .
Let A = R – {2}, B = R – {1}. If f : A → B is a function defined by show that f is one-one and onto. Hence find
Find the equation of tangent to the curve y = cos (x + y), -2π ≤ x ≤ 0, that is parallel to the line x + 2y = 0.
If the function f : R → R is given by f(x) = and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Is f⁻¹ = g?
