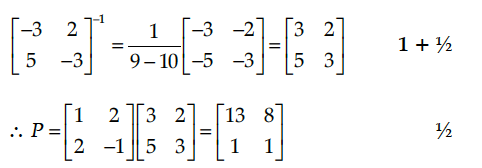
If P(A) = 0.4, P(B) = p, P(A U B) = 0.6 and A and B are given to the independent events, find the value of ‘p’.
The radius r of the base of a right circular cone is decreasing at the rate of 2 cm/min. and height h is increasing at the rate of 3 cm/min. When r = 3.5 cm and h = 6 cm, find the rate of change of the volume of the cone.
If A and B are two independent events, then prove that the probability of occurrence of at least one of A and B is given by 1 – P(A’) · P(B’)
If A and B are two events such that P(A) = 0.4, P(B) = 0.8 and P(B/A) = 0.6, then find P(A/B).
Find the area of the parallelogram whose diagonals are represented by the vectors = and