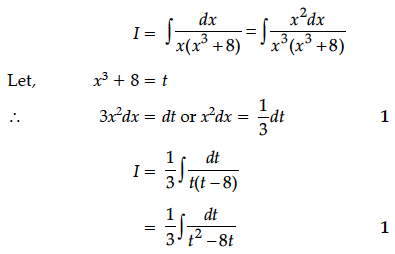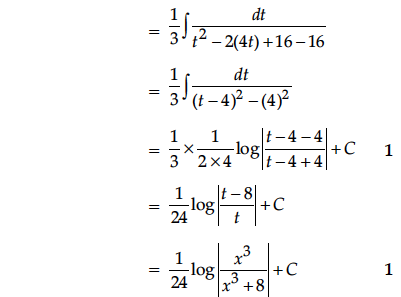Question

Show that a function f : R → R given by f(x) =ax + b,a, b ∈ R, a ≠ 0 is a bijective.

Evaluate : $\large\textstyle\int{\frac{3x+1}{(x^{3}-x^{2}-x+1)}}d x\,.$

Find the general solution of the following differential equation : $y-x{\frac{d y}{d x}}=a\left(y^{2}+{\frac{d y}{d x}}\right).$

Form the differential equation representing family of curves given by (x – a)² + 2y²= a², where a is an arbitrary constant.

Find the particular solution of the differential equation $\log\left(\frac{d y}{d x}\right)=3x+4y,$ given that y = 0, when x = 0.

P speaks truth in 70% of the cases and Q in 80% of the cases. In what percent of cases are they likely to agree in stating the same fact ?

Let f : X -> Y be a function. Define a relation R on X given be R = {(a, b) : f(a) = f(b)}. Show that R is an equivalence relation ?