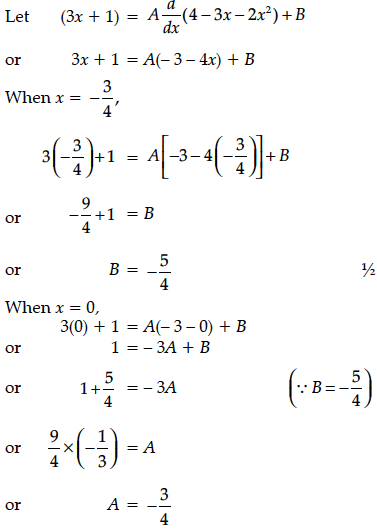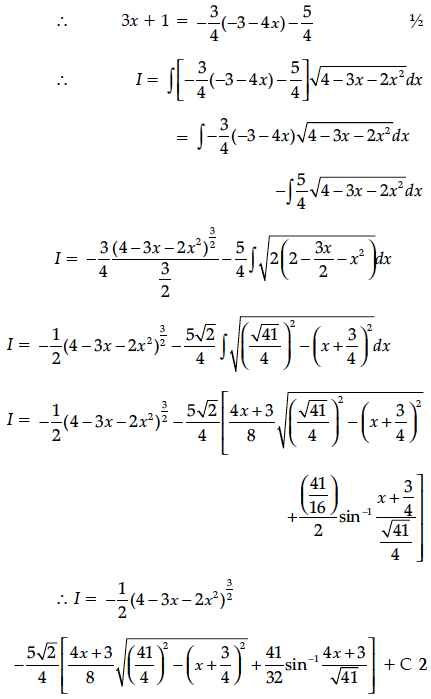Question

Find the solution of the differential equation $(x d y-y d x)\,y\,\mathrm{sin}{\left({\frac{y}{x}}\right)}=(y d x+x d y)x\cos\biggl({\frac{y}{x}}\biggr).$

Find the particular solution of the differential equation : $y e^{y}\,d x=(y^{3}+2x e^{y})d y,y(0)=1$

Find the particular solution of the differential equation : ${\frac{d y}{d x}}\ +y\cot x=2x+x^{2}\cot x,$ x ≠ 0. Given that y = 0, when $x={\frac{\pi}{2}}\ .$

Three schools A, B and C organised a fete (mela) collecting funds for flood victims in which they sold hand-helds fans, mats and toys made from recycled material, the sale price of each being ₹ 25, ₹ 100 and ₹ 50 respectively. The following table shows the number of articles of each type sold :

Find the particular solution of the following differential equation : $x\left(x^{2}-1\right){\frac{d y}{d x}}\ =1;$ y = 0, when x = 2.

Find the particular solution of the following differential equation given that at x = 2, y = 1 $x\,{\frac{d y}{d x}}\,+\,2y=x^{2},\,(x\,\neq\,0).$

Let A = {1, 2, 3, . ...., 9} and R be the relation in A × A defined by (a, b) R (c, d) if a + d =b + c for (a, b), (c, d) in A × A. Prove that R is an equivalence relation. Also obtain the equivalence class [(2, 5)].