If A is a square matrix such that A² = A, then write the value of (I + A)² – 3A.
(I + A)² – 3A = I
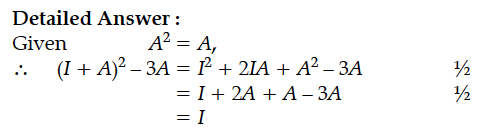
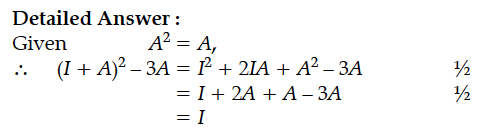
If A is a square matrix such that A² = I, then find the simplified value of (A – I)³ + (A + I)³ – 7A.
If A is a square matrix such that A² = A, then write the value of 7A – (I + A)³, where I is an identity matrix.
Let A and B are matrices of order 3 x 2 and 2 x 4 respectively. Write the order of matrix (AB).
Write the differential equation obtained by eliminating the arbitrary constant C in the equation representing the family of curves xy = C cos x.
L and M are two points with position vectors and respectively. Write the position vectors of a point N which divides the line segment LM in the ratio 2:1 externally.
