If A = , find when is called minor and is called co-factors of A.
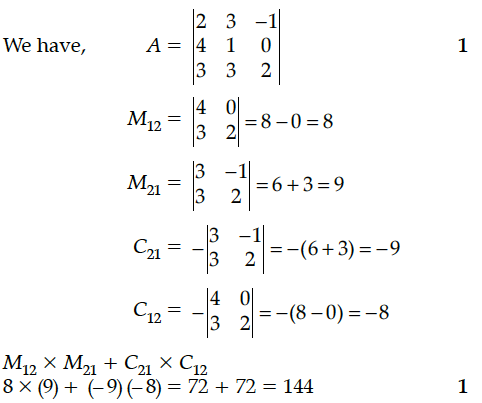
If A = is is a matrix of order 2 × 2, such that |A| = –15, and represents the cofactor of , then find
Show that the function f(x) = x³ – 3x² + 6x – 100 is increasing on R.
If P(E) = 7/13, P(F) = 9/3 and P(E' / F') = 4/3, then evaluate :
(i) P(E / F)
(ii) P(E / F)
Obtain the differential equation of the family of circles passing through the points (a, 0) and (– a, 0).
The radius r of a right circular cylinder is decreasing at the rate of 3 cm/min. and its height h is increasing at the rate of 2 cm/min. When r =7 cm and h = 2 cm, find the rate of change of the volume of cylinder.
A particle moves along the curve 6y = x³ + 2. Find the points on the curve at which y-coordinate is changing 2 times as fast as x-coordinate.
