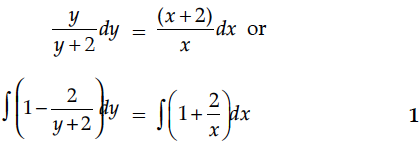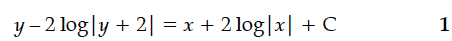Question

The length x, of a rectangle is decreasing at the rate of 5 cm/minute and the width y, is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rate of change of the area of the rectangle.

Find : $\textstyle\int$$\frac{d x}{\sqrt{3-2\,x-x^{2}}}$

If P(E) = 6/11, P(F) = 5/11 and P(E ∪ F) = 7/11 then find (i) P(E/F) (ii) P(F/E)

Find the sum of the order and the degree of the following differential equations : ${\frac{d^{2}y}{d x^{2}}}+{3{\sqrt\frac{{d y}}{d x}}}+(1+x)=0$

Form the differential equation of all circles which is tough the x-axis at the origin.

Find the general solution of the differential equation ${\frac{d y}{d x}}+{\frac{2}{x}}y=x$

The position vectors of points A, B and C are $λ\stackrel{\wedge}{i}+3\stackrel{\wedge}{j}$,$12\stackrel{\wedge}{i}+μ\stackrel{\wedge}{j}$ and $11\stackrel{\wedge}{i}-3\stackrel{\wedge}{j}$ respectively. If C divides the line segment joining A and B in the ratio 3 : 1, find the values of λ and μ.