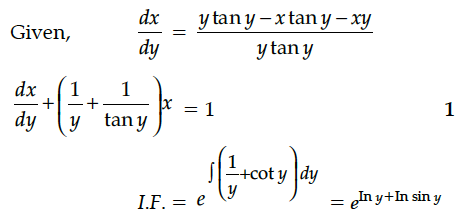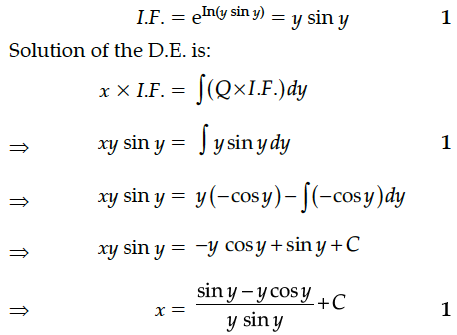Question

Find the particular solution of the differential equation satisfying the given condition ${\frac{d y}{d x}}=y\tan x,$ given that y = 1, when x = 0.

A speaks truth in 75% of the cases, while B in 90% of the cases. In what percent of cases are they likely to contradict each other in stating the same fact ? Do you think that statement of B is always true ?

Find the particular solution of the differential equation ${\frac{d y}{d x}}\ =1+x+y+x y$ given that y = 0 when x = 1.

Let f : X -> Y be a function. Define a relation R on X given be R = {(a, b) : f(a) = f(b)}. Show that R is an equivalence relation ?

Solve the differential equation ${\frac{d y}{d x}}\ +\ y\ \cot\ x$= 2 cos x, given that y = 0 when $x={\frac{\pi}{3}}\,.$

P speaks truth in 70% of the cases and Q in 80% of the cases. In what percent of cases are they likely to agree in stating the same fact ?

Find the general solution of the differential equation (1 + tan y)(dx – dy) + 2xdy = 0.