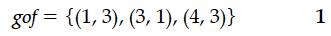
If f : R → R and g : R → R are given by f(x) = sin x and g(x) = 5x² then find gof(x)
State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive.
Let f : X -> Y be a function. Define a relation R on X given be R = {(a, b) : f(a) = f(b)}. Show that R is an equivalence relation ?
If A = {1, 2, 3}, B = {4, 5, 6, 7} and f = {(1, 4), (2, 5),(3, 6)} is a function from A to B. State whether f is one-one or not.
Let R be the equivalence relation in the set A = {0, 1, 2, 3, 4, 5} given by R = {(a, b) : 2 divides (a –b)}. Write the equivalence class [0].
If the following function f(x) is continuous at x = 0, then write the value of k.
Using derivative, find the approximate percentage increase in the area of a circle if its radius is increased by 2%.
Write the value of λ so that the vectors = and = are perpendicular to each other ?