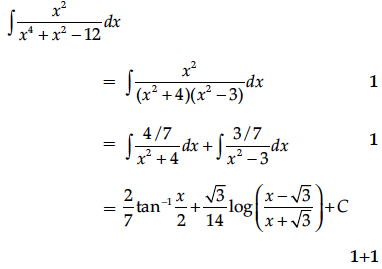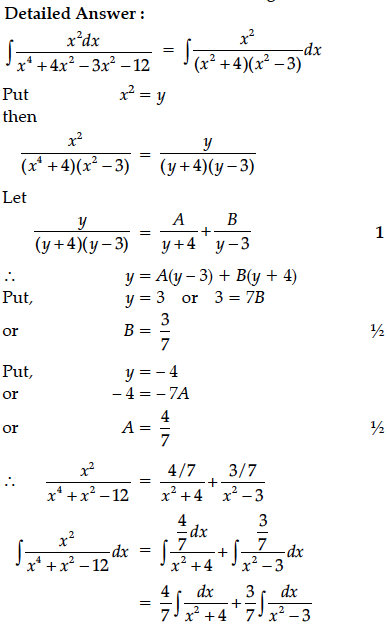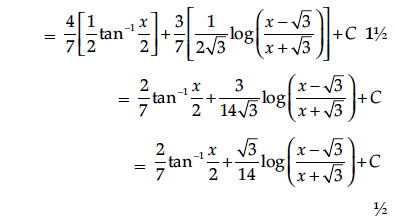Question

Show that the equation of tangent to the parabola y² = 4ax at (x₁, y₁) is yy₁ = 2a(x + x₁).

If Z is the set of all integers and R is the relation on Z defined as R = {(a, b) : a, b ∈ Z and a – b is divisible by 5}. Prove that R is an equivalence relation.

Form the differential equation of the family of circles in the second quadrant and touching the co-ordinate axes.

P speaks truth in 70% of the cases and Q in 80% of the cases. In what percent of cases are they likely to agree in stating the same fact ?

Find the particular solution of the following differential equation : $(x\ +1){\frac{d y}{d x}}=2e^{-y}-1;$ y = 0 when x = 0.

Find the particular solution of the differential equation satisfying the given condition ${\frac{d y}{d x}}=y\tan x,$ given that y = 1, when x = 0.

Show that the equation of normal at any point t on the curve x = 3 cos t – cos³t and y = 3 sin t – sin³t is 4(y cos2t – x sin³t) = 3 sin 4t