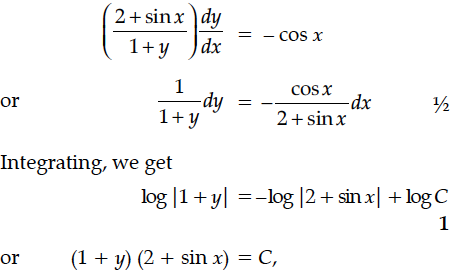
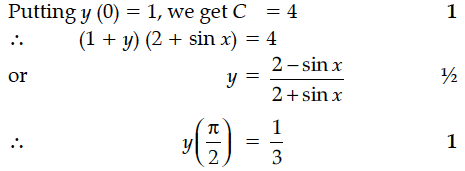
Find the particular solution of the differential equation : x ≠ 0. Given that y = 0, when
Find the particular solution of the differential equation : 4x cosec x, (x ≠ 0), given, that y = 0,when
Show that the equation of normal at any point t on the curve x = 3 cos t – cos³t and y = 3 sin t – sin³t is 4(y cos2t – x sin³t) = 3 sin 4t
A speaks truth in 75% of the cases, while B in 90% of the cases. In what percent of cases are they likely to contradict each other in stating the same fact ? Do you think that statement of B is always true ?
For the curve y = 4x³ – 2x⁵, find all those points at which the tangent passes through the origin.
Let f : N → R be a function defined as f(x) = 4x² + 12x + 15. Then show that f : N → S, where S is range of f, is invertible. Also find the inverse of f.
Show that f : N → N, given by f(x) = |``x+1, if x is odd x- 1, if x is even is both one-one and onto.``|
Find the points on the curve y = x³ – 3x² – 9x + 7 at which the tangent to the curve is parallel to the x-axis.
Find the equation(s) of the tangent(s) to the curve y = (x³ – 1) (x – 2) points where the curve intersects the x-axis.