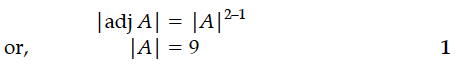If A is an invertible square matrix of order 3 and |A| = 5, then find the value of |adj A|.
If the determinant of matrix A of order 3 × 3 is of value 4, write the value of |3A|.
If A and B are square matrices of order 3 such that |A| = –1, |B| = 3, then find the value of |2AB|.
Let A = {1, 2, 3, 4}. Let R be the equivalence relation on A × A defined by (a, b)R(c, d) if a + d = b + c. Find the equivalence class [(1,3)].