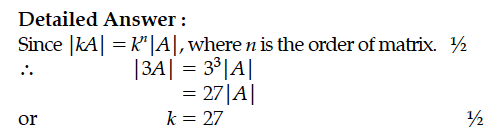If A is an invertible square matrix of order 3 and |A| = 5, then find the value of |adj A|.
If the determinant of matrix A of order 3 × 3 is of value 4, write the value of |3A|.
If A and B are square matrices of order 3 such that |A| = –1, |B| = 3, then find the value of |2AB|.
Write the equation of tangent drawn to the curve y = sin x at the point (0, 0).